Segment Tree+KMP
백준 3308번 Matching 문제풀이
[3308 Matching] https://www.acmicpc.net/problem/3308 .
문자열에서 패턴을 찾을 때 KMP를 이용하는데 세그트리와 접목한 문제를 풀어보자!
내 블로그에 포스팅할때도 KMP랑 Segment tree를 비슷한 시기에 올린 것 같은데 그 둘을 접목한 문제가 있다는 것을 배웠다.
ICPC신촌 캠프할 때 접한 20298 파인애플피자로 이런 유형을 알게 되었다.
이걸 풀어내니 23576 Stock Price Prediction도 풀수 있게 되었다.
결국 KMP를 할때 문자가 같은지 확인하는 부분에서 같은 꼴(비슷한 형태)인지 확인하는 형태로 바꾸면 되는 문제이다.
문제상황 파악하기.
위에서 소개한 두 문제와 정확히 동일하지만 입력의 형태가 좀 다르다.
패턴이 주어지는데 작은 순서대로 인덱스를 주기 때문이다.
예를 들어 2 1 5 3 4처럼 주어지면 2번이 젤 작고 1번, 5번, 3번, 4번 순이라는 뜻이다.
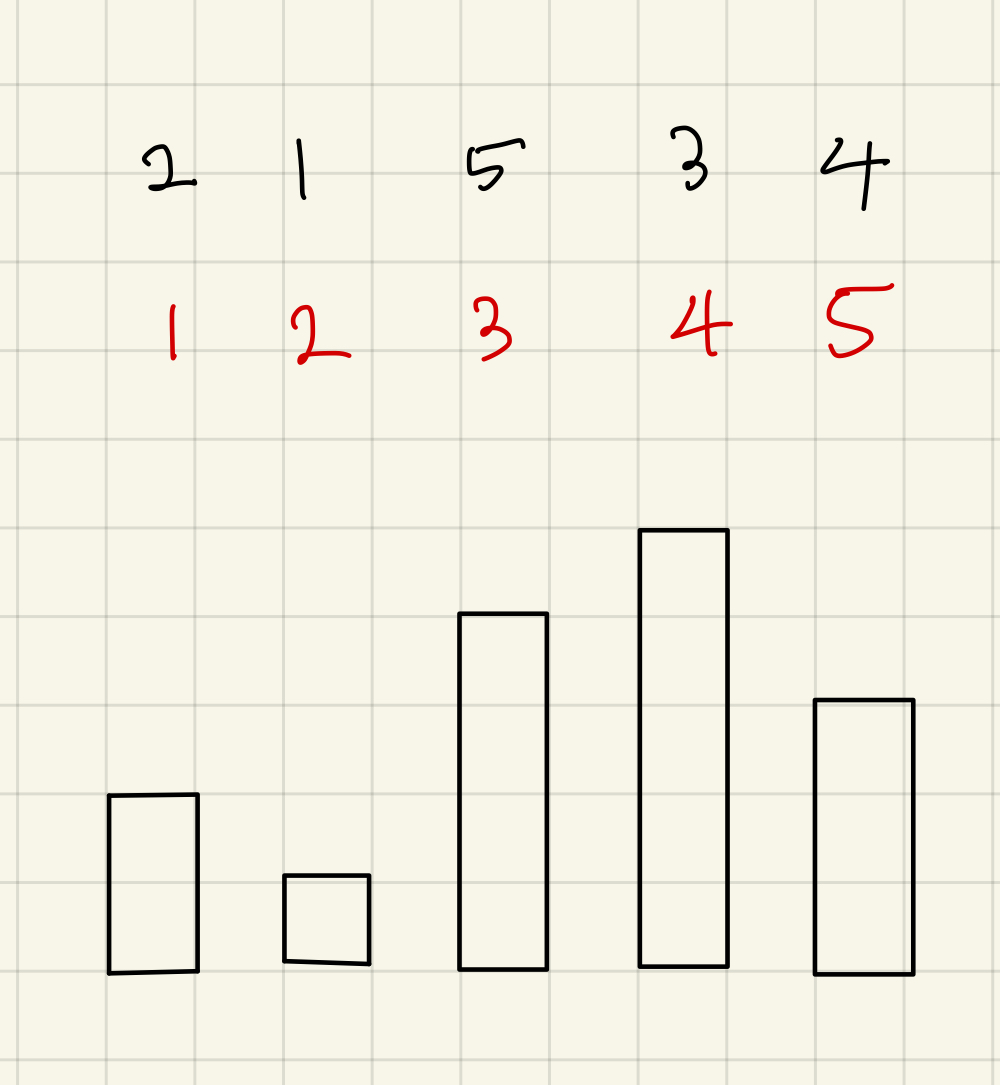
위 그림과 같은 대소관계를 가진 그래프를 찾으면 된다.
이를 그래프 같은 모양의 숫자를 설정해서 파인애플 피자 풀듯이 풀면 끝이다.
아이디어 얻기.
파인애플 피자 풀듯이 풀면 끝이라고는 했지만 파인애플 피자도 포스팅을 안했다. ㅎㅎ
푸는 아이디어는 다음과 같다.
먼저 KMP의 매칭 부분을 잘 보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
for(int i=0, j=0;i<n+k-1;i++){
while (j&&H[i]!=P[j]) j = ff[j-1]; //다르면 failure function에 따라 다시 매칭시작
if(H[i]==P[j]){
if(j==M-1){
ret++; //완벽하게 매칭 됨
j = ff[j];
}else{
j++; //계속 매칭해나감
}
}
}
return ret;
저기서 Hay 문자열과 Pattern 문자열을 비교하는 부분을 바꾸면 된다.
지금 매칭하는 것은 문자열에서의 rank이다.
그니까 1과 100이 같은 rank일지도 모른다는 것이다.
예를 들면 다음과 같은 것이다.
1 2 3 4 5 와 100 200 300 400 500에서 1과 100은 같은 것이다.
그 이유는 1보다 큰게 패턴에서 4개, 100보다 큰게 4개로 같기 때문이다.
그니까 비교를 할 때 비교대상보다 작은것의 개수, 큰 것의 개수를 세어서 그게 일치하면 같은 문자로 보는 것이다.
세그먼트 트리는 구간에 원소가 몇개 있는지를 Log시간에 셀 수 있으니 이를 이용한다.
근데 이문제는 세그트리 안쓰고 O(N+M)에 풀 수 있다.
중복되는 문자(패턴)가 없기 때문에 25008 문자열 찾기이 문제 처럼 풀 수 있기 때문이다.
하지만 연습삼아 세그트리로 풀꺼다.(근데 시간초과 한번 떴음 ㅠㅠ)
논리는 다음과 같다.
- 입력을 받아서 패턴(needle)을 만든다.
- 좌표압축을 통해 패턴(needle)과 hay문자열을 만든다.
- 자기보다 작은 것의 개수 자기보다 큰것의 개수가 같으면 계속 매칭해나간다.
- 매칭이 다 됐으면(패턴의 길이와 같으면) 결과에 idx를 추가한다.
주의할 점
일단 나는 재귀 세그를 짰더니 시간초과가 떴다 ㅠㅠ 비재귀 세그로 다시 짜서 내보니 됐다.
실제 코드
나머지 주의 할 점은 코드에 주석으로 처리했다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <cstring>
#include <stack>
#include <queue>
#include <cmath>
#include <set>
#include <map>
#include <cassert>
#define fast_io cin.tie(NULL); ios_base::sync_with_stdio(false);
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int MAX = 1000001;
struct Fenwick{
int n;
int t[2 * MAX];
void modify(int p, int value) { // plus value at position p
for (t[p += n] += value; p > 1; p >>= 1) t[p>>1] = t[p] + t[p^1];
}
int query(int l, int r) { // sum on interval [l, r)
int res = 0;
for (l += n, r += n; l < r; l >>= 1, r >>= 1) {
if (l&1) res += t[l++];
if (r&1) res += t[--r];
}
return res;
}
void clear(){
for(int i=0;i<2*MAX;i++) t[i] = 0;
}
};
int m, n;
vector<int> x, y, X, Y, res, front, back, temp;
Fenwick fwt;
bool Match(int i, int j, int sz){
if(front[j]!=fwt.query(0, i)) return false;
if(back[j]!=fwt.query(i+1, MAX)) return false;
return true;
}
vector<int> getFail(vector<int> &P){
int sz = P.size();
vector<int> Fail(sz);
for(int i=0;i<sz;i++){
front[i] = fwt.query(0, P[i]);
back[i] = fwt.query(P[i]+1, MAX);
fwt.modify(P[i], 1);
}
fwt.clear();
for(int i=1, j=0;i<sz;i++){
while (j&&!Match(P[i], j, sz)) {
for(int k=i-j;k<i-Fail[j-1];k++) fwt.modify(P[k], -1);
j = Fail[j-1];
}
if(Match(P[i], j, sz)){
Fail[i] = ++j;
fwt.modify(P[i], 1);
}
}
return Fail;
}
void KMP(vector<int> &H, vector<int> &P){
int hsz = H.size(), psz = P.size();
vector<int> ff = getFail(P);
fwt.clear();
for(int i=0, j=0;i<hsz;i++){
while (j&&!Match(H[i], j, hsz)) {
for(int k=i-j;k<i-ff[j-1];k++) fwt.modify(H[k], -1);
j = ff[j-1];
}
if(Match(H[i], j, hsz)){
if(j==psz-1){
res.push_back(i-psz+2);
for(int k=i-j;k<i-ff[j]+1;k++) fwt.modify(H[k], -1);
fwt.modify(H[i], 1);
j = ff[j];
}else{
j++;
fwt.modify(H[i], 1);
}
}
}
}
void compress(){
sort(x.begin(), x.end());
x.erase(unique(x.begin(), x.end()) ,x.end());
for(int i=0;i<m;i++) X[i] = lower_bound(x.begin(), x.end(), X[i])-x.begin()+1;
sort(y.begin(), y.end());
y.erase(unique(y.begin(), y.end()), y.end());
for(int i=0;i<n;i++) Y[i] = lower_bound(y.begin(), y.end(), Y[i])-y.begin()+1;
}
int main(){
fast_io
cin >> m >> n;
x = vector<int> (m); X = vector<int> (m);
y = vector<int> (n); Y = vector<int> (n);
temp = vector<int> (m);
for(int i=0;i<m;i++){
cin >> temp[i];
x[temp[i]-1] = X[temp[i]-1] = i+1;
}
for(int i=0;i<n;i++){
cin >> y[i]; Y[i] = y[i];
}
compress();
front = vector<int> (m);
back = vector<int> (m);
fwt.n = MAX;
KMP(Y, X);
cout << res.size() << '\n';
for(int i=0;i<res.size();i++) cout << res[i] << ' ';
}