I am dosa.

Heavy-Light decomposition

HLD(Heavy Light Decomposition)

구현과정

구현과정은 jinhan님의 블로그 를 참고하여 구현했다.

  1. 가중치가 있는 그래프라면 adj에 가중치 없는 그래프를 만들고, cost[정점]에 해당 정점으로 갈 때 드는 비용을 저장한다. 그리고 input[i] = {u, v}이런 식으로 정점에 번호를 붙여준다.(세그트리로 다루기 위함)
  2. dfs1을 돌면서 각 정점의 깊이(dep), 각 정점의 부모 정점(par), 각 정점이 만드는 서브트리 크기(sz)를 저장한다. 이 때 adj[정점][0]에는 가장 무거운 간선이 되도록 한다.
  3. dfs2를 돌면서 오일러투어 테크닉을 적용하고 정점이 무거운 간선을 지니는 정점인지를 체크한다. (top)

정리해보면

  • input[i] = i번째 정점은 {xx정점, yy정점}를 잇는 간선입니다.
  • inp[i] : 직접 입력 받은 가중치가 있는 인접 리스트 그래프
  • adj[i] : inp을 바꿔서 가중치를 떼어낸 그래프
  • cost[i] : i번 째 정점까지 가는데 드는 가중치(비용)
  • dep, par, sz는 위에 설명했고
  • in, out → 오일러 투어 테크닉(DFS ordering)하고 난 결과 in[어떤 정점]이 지칭하는 간선 번호
  • top[i] : i번 정점이 무거운 간선을 포함하면 0 아니면 무거운 간선을 포함하는 정점을 저장해둠.

이제 우리의 문제를 해결해보자!

  1. 두 정점을 잇는 경로에서 가장 큰 가중치를 가진 간선은 무엇일까?
  2. 이 때, 간선의 가중치는 변할 수 있다. → 13510 트리와 쿼리

위의 문제를 해결할 것 이다.

//update 연산 , xst는 maxSegmentTree이다.
// i 번 간선을 val로
    void update(T i, T val){
        if(dep[input[i].xx] < dep[input[i].yy]) swap(input[i].xx, input[i].yy);
        xst.update(in[input[i].xx], val, 1, 1, n);
    }

위 코드를 보면 dep가 깊은 정점에 해당하는 간선을 val로 변화시킨다. 2번에 해당하는 코드이다.

//query 연산
//u, v위 가장 큰 가중치
    T query(T u, T v){
        T ret = 0;
        while(top[u]!=top[v]){
            if(dep[top[u]] < dep[top[v]]) swap(u, v);
            int st = top[u];
            ret = max(ret, xst.xquery(in[st], in[u], 1, 1, n));
            u = par[st];
        }
        if(u==v) return ret;
        if(dep[u] > dep[v]) swap(u, v);
        T nxt = -1;
        for(auto i : adj[u]) if(top[i]==top[u]) nxt = i;
        ret = max(ret, xst.xquery(in[nxt], in[v], 1, 1, n));
        return ret;
    }

이는 1번 - 즉 경로에서 가장 큰 가중치를 구하는 쿼리이다.

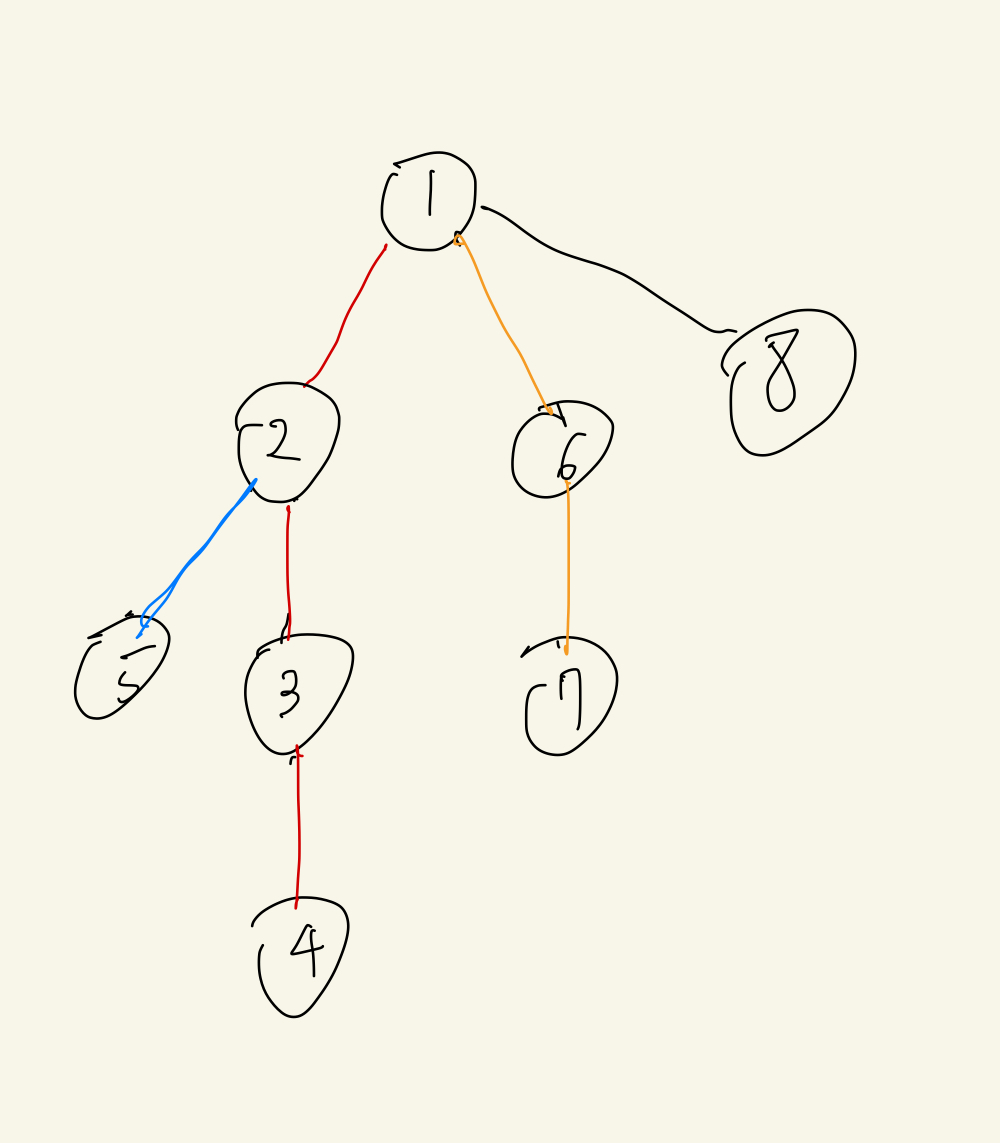
HLD.jpeg

top[어떤 정점]은 간선 분류의 맨 위로 올라간다는 뜻이다.

예를 들어 5 - 7로 간다고 하면

  1. 5랑 7의 깊이가 같으니까 u = 5, v = 7
  2. u를 st = top[u] = 2이다. 파란 간선이 끝나는 정점까지 가고
  3. 이 때 세그먼트 트리로 경로 상 파란 간선을 모두 더한다(최대값을 찾는다).
  4. 다음엔 u = 7, v = 2가 될 것이고 top[u] = 1이다. → 경로 상 노란간선을 모두 더한다.(최대값을 찾는다)
  5. 다음엔 u = 2, v = 1이 될 것이고 top[2] = 1이다. → 경로 상 빨간 간선을 모두 더한다.(최대값을 찾는다)

이런 식으로 무거운 간선을 통해 분류한 간선으로 쭉쭉 이동하면서 처리하는 것이 HLD이다.

이때 이 간선의 종류가 $logN$개 이므로 세그먼트 트리를 하는 $logN$과 합쳐

총 시간 복잡도 : $O((logN)^2)$으로 각 쿼리를 해결 할 수 있는 것이다.

13309 트리

트리가 가중치 1로 모두 연결 되어있다고 하고 연결이 끊어지면 update연산으로 해당간선의 가중치를 0으로 바꿔준다. 그리고나서 구한 경로의 길이가 $dep[u] + dep[v] - dep[lca(u, v)]$ 와 같다면 경로가 존재하는 것이고 나머지 경우는 경로가 존재하지 않는 것이다.

코드는 아래와 같다.

#include <bits/stdc++.h>
#define fast_io cin.tie(NULL); ios_base::sync_with_stdio(false);
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef tuple<int, int, int> tiii;
#define xx first
#define yy second

const int MAXSIZE = 2e5+1;

// 구간합 세그
template <class T>
class Segtree{
public:
    static const int TREESIZE = 4*MAXSIZE;
    T* tree = new T[TREESIZE];

    Segtree(){
        for(int i=0;i<TREESIZE;i++) tree[i] = 0;
    }
    ~Segtree(){
        delete[] tree;
    }
    T update(T x, T v, T node, T S, T E){
        if(S==E) return tree[node] = v; // 원소교체연산, 더하기면 +하셈
        
        T mid = (S+E)>>1;
        if(x<=mid) update(x, v, 2*node, S, mid);
        else update(x, v, 2*node+1, mid+1, E);
        return tree[node] = tree[2*node]+tree[2*node+1];
    }
    T kth(T node, T S, T E, T K){
        if(S==E) return S;
        T mid = (S+E)>>1;
        if(tree[2*node]>=K) return kth(2*node, S, mid, K);
        else return kth(2*node+1, mid+1, E, K-tree[2*node]);
    }
    T query(T L, T R, T node, T S, T E){
        if(L>E||R<S) return 0;
        if(L<=S&&E<=R) return tree[node];
        T mid = (S+E)>>1;
        return query(L, R, 2*node, S, mid)+query(L, R, 2*node+1, mid+1, E);
    }
};
// 경로 중 최대값 찾기
template <class T>
class HLD{
public:
    int n;
    T cost[MAXSIZE], sz[MAXSIZE], dep[MAXSIZE], par[MAXSIZE];
    T top[MAXSIZE], in[MAXSIZE], out[MAXSIZE];
    vector<pair<T, T>> input, inp[MAXSIZE];
    vector<T> adj[MAXSIZE];
    
    bool visited[MAXSIZE];
    
    void dfs(int now = 1){
        visited[now] = 1;
        for(auto [ncost, nxt] : inp[now]){
            if(visited[nxt]) continue;
            adj[now].push_back(nxt);
            cost[nxt] = ncost;
            dfs(nxt);
        }
    }
    
    void dfs1(int now = 1){
        sz[now] = 1;
        for(T& nxt : adj[now]){
            dep[nxt] = dep[now]+1;
            par[nxt] = now;
            dfs1(nxt);
            sz[now] += sz[nxt];
            if(sz[nxt]>sz[adj[now][0]]) swap(nxt, adj[now][0]); //adj[now][0]에는 가장큰것 (heavy)
        }
    }
    
    int tmp = 0;
    void dfs2(int now = 1){
        in[now] = ++tmp;
        for(T nxt : adj[now]){
            top[nxt] = (nxt==adj[now][0] ? top[now] : nxt);
            dfs2(nxt);
        }
        out[now] = tmp;
    }
    
    Segtree<T> st;
    
    // i 번 간선을 val로
    void update(T i, T val){
        if(dep[input[i].xx] < dep[input[i].yy]) swap(input[i].yy, input[i].xx);
        st.update(in[input[i].xx], val, 1, 1, n);
    }
    
    //u, v위 가장 큰 가중치
    T query(T u, T v){
        T ret = 0;
        while(top[u]!=top[v]){
            if(dep[top[u]] < dep[top[v]]) swap(u, v);
            int ST = top[u];
            ret += st.query(in[ST], in[u], 1, 1, n);
            u = par[ST];
        }
        if(u==v) return ret;
        if(dep[u] > dep[v]) swap(u, v);
        ret += st.query(in[u], in[v], 1, 1, n);
        int LCA = lca(u, v);
        ret -= st.query(in[LCA], in[LCA], 1, 1, n);
        return ret;
    }
    
    int lca(int u, int v) {
        while (top[u] != top[v]) {
            if (dep[top[u]] < dep[top[v]]) swap(u, v);
            u = par[top[u]];
        }
        if (dep[u] > dep[v]) swap(u, v);
        return u;
    }
    
    void precal(){
        input = vector<pair<T, T> > (n+1);
        for(int i=2;i<=n;i++){
            int p; cin >> p;
            input[i-1] = {p, i};
            inp[p].push_back({1, i});
            inp[i].push_back({1, p});
        }
        for(int i=1;i<=n;i++){
            st.update(i, 1, 1, 1, n);
        }
        top[1] = 1;
        dfs(); dfs1(); dfs2();
    }
};
HLD<int> hld;

int main(){
    fast_io
    int n, q; cin >> n >> q;
    hld.n = n;
    hld.precal();
    while (q--) {
        int u, v, o; cin >> u >> v >> o;
        bool ok = false;
        if(hld.query(u, v)==hld.dep[u]+hld.dep[v]-2*hld.dep[hld.lca(u, v)]){
            ok = true;
            cout << "YES\n";
        }else{
            cout << "NO\n";
        }
        if(o){
            if(ok) hld.st.update(hld.in[u], 0, 1, 1, n);
            else hld.st.update(hld.in[v], 0, 1, 1, n);
        }
        
    }
}

13512 트리와 쿼리3

  1. 1번 쿼리는 트리의 색을 바꾸는 연산은 XOR 1연산을 통해 해결 할 수 있을 것이다.
  2. 2번 쿼리는 1번 부터 해당 정점으로 가면서 가장 먼저 나오는 1을 찾으면 된다.

2번 쿼리를 처리하는 것이 문제인데…

가장 먼저 나오는 1을 구하는 방법은 이분 탐색을 이용하면 된다.

T bisearch(T L, T R){
        if(!query(L, R, 1, 1, MAXSIZE)) return -1;
        T lo = L-1 , hi = R;
        while(lo+1<hi){
            T mid = (lo+hi)>>1;
//L부터 검사하는게 중요!! lo는 off-by-one error땜에 1을 뺏음
            if(query(L, mid, 1, 1, MAXSIZE)){
                hi = mid;
            }else{
                lo = mid;
            }
        }
        return hi;
    }

이를 이용하여 구간에 1이 존재하지 않으면 바로 -1 리턴

구간에 존재하면 가장 먼저나오는 곳의 dfs order 번호를 리턴한다.

문제는 가장 먼저 1이 나오는 곳의 정점 idx를 출력하는 것이기 때문에 dfs ordering을 할 때 역함수를 구해놓는 것이 편하다. 나는 R이라는 배열을 이용했다.

#include <bits/stdc++.h>
#define fast_io cin.tie(NULL); ios_base::sync_with_stdio(false);
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef tuple<int, int, int> tiii;
#define xx first
#define yy second

const int MAXSIZE = 1e5+1;

// 구간합 세그
template <class T>
class Segtree{
public:
    static const int TREESIZE = 4*MAXSIZE;
    T* tree = new T[TREESIZE];

    Segtree(){
        for(int i=0;i<TREESIZE;i++) tree[i] = 0;
    }
    ~Segtree(){
        delete[] tree;
    }
    T update(T x, T v, T node, T S, T E){
        if(S==E) return tree[node] ^= v; // 원소교체연산, 더하기면 +하셈
        
        T mid = (S+E)>>1;
        if(x<=mid) update(x, v, 2*node, S, mid);
        else update(x, v, 2*node+1, mid+1, E);
        return tree[node] = tree[2*node]+tree[2*node+1];
    }
    T kth(T node, T S, T E, T K){
        if(S==E) return S;
        T mid = (S+E)>>1;
        if(tree[2*node]>=K) return kth(2*node, S, mid, K);
        else return kth(2*node+1, mid+1, E, K-tree[2*node]);
    }
    T query(T L, T R, T node, T S, T E){
        if(L>E||R<S) return 0;
        if(L<=S&&E<=R) return tree[node];
        T mid = (S+E)>>1;
        return query(L, R, 2*node, S, mid)+query(L, R, 2*node+1, mid+1, E);
    }
    T bisearch(T L, T R){
        if(!query(L, R, 1, 1, MAXSIZE)) return -1;
        T lo = L-1 , hi = R;
        while(lo+1<hi){
            T mid = (lo+hi)>>1;
            if(query(L, mid, 1, 1, MAXSIZE)){
                hi = mid;
            }else{
                lo = mid;
            }
        }
        return hi;
    }
};
// 경로 중 최대값 찾기
template <class T>
class HLD{
public:
    int n;
    T cost[MAXSIZE], sz[MAXSIZE], dep[MAXSIZE], par[MAXSIZE];
    T top[MAXSIZE], in[MAXSIZE], out[MAXSIZE];
    T R[MAXSIZE]; //in의 역함수를 설정했음
    vector<pair<T, T>> input, inp[MAXSIZE];
    vector<T> adj[MAXSIZE];
    
    bool visited[MAXSIZE];
    
    void dfs(int now = 1){
        visited[now] = 1;
        for(auto [ncost, nxt] : inp[now]){
            if(visited[nxt]) continue;
            adj[now].push_back(nxt);
            cost[nxt] = ncost;
            dfs(nxt);
        }
    }
    
    void dfs1(int now = 1){
        sz[now] = 1;
        for(T& nxt : adj[now]){
            dep[nxt] = dep[now]+1;
            par[nxt] = now;
            dfs1(nxt);
            sz[now] += sz[nxt];
            if(sz[nxt]>sz[adj[now][0]]) swap(nxt, adj[now][0]); //adj[now][0]에는 가장큰것 (heavy)
        }
    }
    
    int tmp = 0;
    void dfs2(int now = 1){
        in[now] = ++tmp;
        R[tmp] = now;
        for(T nxt : adj[now]){
            top[nxt] = (nxt==adj[now][0] ? top[now] : nxt);
            dfs2(nxt);
        }
        out[now] = tmp;
    }
    
    Segtree<T> st;
    
    // i 번 간선을 val로
    void update(T i, T val){
        if(dep[input[i].xx] < dep[input[i].yy]) swap(input[i].yy, input[i].xx);
        st.update(in[input[i].xx], val, 1, 1, n);
    }
    
    //u, v위 가장 먼저나오는 1
    T query(T u, T v){
        T ret = -1;
        while(top[u]!=top[v]){
            if(dep[top[u]] < dep[top[v]]) swap(u, v);
            int ST = top[u];
            int now = st.bisearch(in[ST], in[u]);
            if(now>0) ret = now;
            u = par[ST];
        }
            
        if(dep[u] > dep[v]) swap(u, v);
        int now = st.bisearch(in[u], in[v]);
        if(now>0) ret = now;
        return ((ret==-1) ? ret : R[ret]);
    }
    
    int lca(int u, int v) {
        while (top[u] != top[v]) {
            if (dep[top[u]] < dep[top[v]]) swap(u, v);
            u = par[top[u]];
        }
        if (dep[u] > dep[v]) swap(u, v);
        return u;
    }
    
    void precal(){
        input = vector<pair<T, T> > (n+1);
        for(int i=2;i<=n;i++){
            int u, v; cin >> u >> v;
            input[i-1] = {u, v};
            inp[u].push_back({1, v});
            inp[v].push_back({1, u});
        }
        top[1] = 1;
        dfs(); dfs1(); dfs2();
    }
};
HLD<int> hld;

int main(){
    fast_io
    int n, q; cin >> n;
    hld.n = n;
    hld.precal();
    cin >> q;
    while (q--) {
        int op, v; cin >> op >> v;
        if(op==1){
            hld.st.update(hld.in[v], 1, 1, 1, MAXSIZE);
        }else{
            cout << hld.query(1, v) << '\n';
        }
    }
}

2927 남극탐험

우리는 트리 구조가 확정된 상태에서 HLD를 이용하여 문제를 풀었지만 이 문제는 트리 구조가 완성되어 있지 않다. 이런 경우 완성 되었을 때의 문제로 치환을 하는 것이 필요하다.

이 때 오프라인 쿼리를 이용할 수 있다.

일단, bridge연산은 Union Find를 떠올릴 수 있다. 그렇기 때문에 이 연산을 통해 만들어진 그래프는 무조건 트리 형태이다. 하지만 bridge연산이 정확히 n-1개의 yes가 나온다는 보장이 없기 때문에 여러 트리가 만들어 질 수 있다. 여러 트리를 합쳐서 하나의 트리를 만드는 아이디어를 떠올릴 수 있었다.

이제 excursion 연산에 대해 고민해보자.

excursion은 일단 길이 없으면 “inpossible”을 출력한다. 근데 이 경우는 그냥 순서대로 보면서도 해결 할 수 있다. 나머지 길이 있는 경우는 트리에서는 정점 u, v 사이의 길이 하나 밖에 없기 때문에 그냥 HLD이용하면 된다.

결론 :

→ 순서대로 보면서 excursion중에 불가능한 거는 미리 골라 둔다.

→ 이제 완성된 트리를 가지고 쿼리를 거꾸로 보면서 경로 쿼리로 길이 있는 경우를 계산한다.

→ penguins 연산은 역으로 돌아가는 식으로 해야한다. (세그먼트 트리 update하면 된다. )

  • 마지막으로 결과를 출력할 때
    • bridge라면
      • 미리 저장된 1 → yes 0 → no
    • penguins라면
      • continue
    • excursion라면
      • Unionfind로 평가했을 때 이미 -1 → “impossible”
      • 그게 아니라면 query(a, b)

자세한건 아래 코드에서 주석 처리로 보이겠다.

#include <bits/stdc++.h>
#define fast_io cin.tie(NULL); ios_base::sync_with_stdio(false);
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef tuple<int, int, int> tiii;
#define xx first
#define yy second

const int MAXSIZE = 3e4+1;
int P[MAXSIZE];

struct DisjointSet{
    vector<int> parent, rank;
    
    DisjointSet(int n):parent(n+1),rank(n+1, 0){
        for(int i=0;i<=n;i++){
            parent[i] = i;
        }
    }
    
    int find(int u){
        if(u==parent[u]) return u;
        return parent[u] = find(parent[u]);
    }
    
    bool merge(int u, int v){
        u = find(u);
        v = find(v);
        if(u==v) return true;
        
        if(rank[u]>rank[v]) swap(u, v);
        parent[u] = v;
        if(rank[u]==rank[v]) rank[v]++;
        return false;
    }
    bool check(int u, int v){
        u = find(u);
        v = find(v);
        if(u==v) return true;
        return false;
    }
};

// 구간합 세그
template <class T>
class Segtree{
public:
    static const int TREESIZE = 4*MAXSIZE;
    T* tree = new T[TREESIZE];

    Segtree(){
        for(int i=0;i<TREESIZE;i++) tree[i] = 0;
    }
    ~Segtree(){
        delete[] tree;
    }
    T update(T x, T v, T node, T S, T E){
        if(S==E) return tree[node] = v; // 원소교체연산, 더하기면 +하셈
        
        T mid = (S+E)>>1;
        if(x<=mid) update(x, v, 2*node, S, mid);
        else update(x, v, 2*node+1, mid+1, E);
        return tree[node] = tree[2*node]+tree[2*node+1];
    }
    T kth(T node, T S, T E, T K){
        if(S==E) return S;
        T mid = (S+E)>>1;
        if(tree[2*node]>=K) return kth(2*node, S, mid, K);
        else return kth(2*node+1, mid+1, E, K-tree[2*node]);
    }
    T query(T L, T R, T node, T S, T E){
        if(L>E||R<S) return 0;
        if(L<=S&&E<=R) return tree[node];
        T mid = (S+E)>>1;
        return query(L, R, 2*node, S, mid)+query(L, R, 2*node+1, mid+1, E);
    }
};
// 경로 중 최대값 찾기
template <class T>
class HLD{
public:
    int n;
    T cost[MAXSIZE], sz[MAXSIZE], dep[MAXSIZE], par[MAXSIZE];
    T top[MAXSIZE], in[MAXSIZE], out[MAXSIZE];
    vector<pair<T, T>> input, inp[MAXSIZE];
    vector<T> adj[MAXSIZE];
    
    bool visited[MAXSIZE];
    
    void dfs(int now = 0){
        visited[now] = 1;
        for(auto [ncost, nxt] : inp[now]){
            if(visited[nxt]) continue;
            adj[now].push_back(nxt);
            cost[nxt] = ncost;
            dfs(nxt);
        }
    }
    
    void dfs1(int now = 0){
        sz[now] = 1;
        for(T& nxt : adj[now]){
            dep[nxt] = dep[now]+1;
            par[nxt] = now;
            dfs1(nxt);
            sz[now] += sz[nxt];
            if(sz[nxt]>sz[adj[now][0]]) swap(nxt, adj[now][0]); //adj[now][0]에는 가장큰것 (heavy)
        }
    }
    
    int tmp = -1;
    void dfs2(int now = 0){
        in[now] = ++tmp;
        for(T nxt : adj[now]){
            top[nxt] = (nxt==adj[now][0] ? top[now] : nxt);
            dfs2(nxt);
        }
        out[now] = tmp;
    }
    
    Segtree<T> st;
    
    // i 번 간선을 val로
    void update(T i, T val){
        if(dep[input[i].xx] < dep[input[i].yy]) swap(input[i].yy, input[i].xx);
        st.update(in[input[i].xx], val, 1, 0, n);
    }
    
    //u, v경로상 펭귄의 수
    T query(T u, T v){
        T ret = 0;
        while(top[u]!=top[v]){
            if(dep[top[u]] < dep[top[v]]) swap(u, v);
            int ST = top[u];
            ret += st.query(in[ST], in[u], 1, 0, MAXSIZE);
            u = par[ST];
        }
        if(dep[u] > dep[v]) swap(u, v);
        ret += st.query(in[u], in[v], 1, 0, MAXSIZE);
        return ret;
    }
    
    int lca(int u, int v) {
        while (top[u] != top[v]) {
            if (dep[top[u]] < dep[top[v]]) swap(u, v);
            u = par[top[u]];
        }
        if (dep[u] > dep[v]) swap(u, v);
        return u;
    }
    
    void precal(){
        for(int i=1;i<=n;i++){
            inp[0].push_back({1, i});
            inp[i].push_back({1, 0});
        }
        
        top[0] = 1;
        dfs(); dfs1(); dfs2();
    }
};

DisjointSet uf(MAXSIZE);
HLD<int> hld;

class Data{
public:
    string op;
    int a, b ,idx, p,q;
};

pair<string, int> ans[300005];
int main(){
    fast_io
    int n; cin >> n;
    hld.n = n;
    for(int i=1;i<=n;i++) cin >> P[i];
    int q; cin >> q;
    vector<Data> Q(q+1);
    for(int i=1;i<=q;i++){
        string op;
        int a, b;
        cin >> op >> a >> b;
        if(op=="bridge"){
            if(uf.merge(a, b)){//이미 합쳐져있음
                ans[i] = {"bridge", 0};
            }else{//합쳐야함
                ans[i] = {"bridge", 1};
                hld.inp[a].push_back({1, b});
                hld.inp[b].push_back({1, a});
            }
            Q[i] = {op, a, b, i, -1, -1};
            
        }else if(op=="penguins"){
            Q[i] = {op, a, b, i, P[a], b};
            P[a] = b;
        }else{
            if(uf.check(a, b)){ //이미 합쳐져 있음
                Q[i] = {op, a, b, i, a, b};
            }else{
                ans[i] = {"excursion", -1};
                Q[i] = {op, a, b, i, -1, -1};
            }
        }
    }
    
    hld.precal();   //0이 루트인 하나의 트리
    for(int i=1;i<=n;i++){ //펭귄을 각 섬에 넣어줌
        hld.st.update(hld.in[i], P[i], 1, 0, MAXSIZE);
    }
    
    
    for(int i=q;i>=1;i--){
        if(Q[i].op=="bridge") continue;
	        if(Q[i].op=="penguins"){
            hld.st.update(hld.in[Q[i].a], Q[i].p, 1, 0, MAXSIZE);
            ans[Q[i].idx] = {Q[i].op, 0};
        }else{
            if(Q[i].p==-1) continue;
            ans[Q[i].idx] = {Q[i].op, hld.query(Q[i].a, Q[i].b)};
        }
    }
    
    for(int i=1;i<=q;i++){
        if(ans[i].xx=="bridge"){
            if(ans[i].yy) cout << "yes\n";
            else cout << "no\n";
        }else if(ans[i].xx=="penguins"){
            continue;
        }else{
            if(ans[i].yy==-1) cout << "impossible\n";
            else cout << ans[i].yy << '\n';
        }
    }
}

Leave a comment

2024

D&C Optimization

3 minute read

분할정복을 이용한 다이나믹 프로그래밍 최적화

Back to top ↑

2023

Back to top ↑

2022

Greedy

2 minute read

백준 18186번 라면사기(large) 문제풀이

SCC

2 minute read

백준 4196번 도미노 문제풀이

LCA

2 minute read

백준 3176번 도로 네트워크 문제풀이

2-SAT

2 minute read

백준 16367번 TV Show Game 문제풀이

Hashing

2 minute read

백준 21162번 뒤집기 K 문제풀이

Tree DP

1 minute read

백준 1949번 우수 마을 문제풀이

Trie

1 minute read

Trie 자료구조 이해하기

Merge Sort

1 minute read

merge sort를 이용하여 inversion 개수세기

Segment Tree

2 minute read

백준 11505 구간 곱 구하기 문제풀이

BFS

1 minute read

백준 2206 벽 부수고 이동하기 문제풀이

기하

1 minute read

백준 2166 다각형의 면적 문제풀이

이분탐색

1 minute read

백준 12015 가장 긴 증가하는 부분 수열2 문제풀이

누적 합

1 minute read

백준 10986 나머지합 문제풀이

Stack

1 minute read

스택 구현하기 ========== 자료구조의 기본이라고 하면 스택 과 큐가 있다 백준 10828번에서 마주친 스택

정렬1

1 minute read

매우매우 많은 정렬이 있지만 그중 가장 안 어려운 3가지를 공부해보았다.

Back to top ↑